Rumus Hubungan Roda-Roda Sepusat
Dalam hubungan roda-roda sepusat, kecepatan sudut roda besar dan roda kecil akan selalu sama. Karena itu, persamaannya bisa elo tulis sebagai berikut.
⍵A = kecepatan sudut roda kecil atau roda kuning
⍵B = kecepatan sudut roda besar atau roda ungu
Dari persamaan di atas, ada satu hal yang perlu elo ingat. Meskipun kecepatan sudut mereka sama, kedua roda punya ukuran jari-jari yang berbeda. Otomatis, kecepatan linearnya akan berbeda juga.
Jadi, dari persamaan tersebut, elo bisa mengetahui perbandingan kecepatan linear roda ungu dan kuning sebagai berikut.
⍵A = kecepatan sudut roda kecil atau roda kuning
⍵B = kecepatan sudut roda besar atau roda ungu
VA = kecepatan linear roda kecil atau roda kuning
VB= kecepatan linear roda besar atau roda ungu
RA= jari-jari roda kecil atau roda kuning
RB= jari-jari roda besar atau roda ungu
Baca Juga: Materi Lengkap Besaran dan Satuan Fisika Kelas 10
Contoh Soal Perhitungan Keliling Lingkaran
Melansir smpn3payakumbuh.sch.id, berikut contoh soal dan pembahasan keliling lingkaran:
Hitunglah keliling lingkaran yang mempunyai diameter 15 cm dengan π = 3,14.
Keliling = πd = 3,14 x 15 cm = 47,1 cm.
Hitunglah diameter lingkaran yang mempunyai keliling 25,12 cm dan π = 3,14.
Jadi, diameter lingkaran tersebut adalah 8 cm.
Tentukan keliling lingkaran yang berdiameter 21 cm dan π = 22/7.
Keliling = πd = 22/7 x 21 cm = 22 x 3 cm = 66 cm.
Tentukan keliling lingkaran yang berdiameter 35 cm dan π = 22/7.
Keliling = πd = 22/7 x 35 cm = 22 x 5 cm = 110 cm.
Tentukan keliling lingkaran yang berdiameter 49 cm dan π = 22/7.
Keliling = πd = 22/7 x 49 cm = 22 x 7 cm = 154 cm.
Tentukan keliling lingkaran yang berdiameter 38,5 cm dan π = 22/7/
Keliling = πd = 22/7 x 38,5 cm = 22 x 5,5 cm = 121 cm.
Tentukan keliling lingkaran yang panjang jari-jarinya 10 cm dan π = 3,14.
Keliling = 2πr = 2 x 3,14 x 10 cm = 62,8 cm.
Tentukan keliling lingkaran yang panjang jari-jarinya 15 cm dan π = 3,14.
Keliling = 2πr = 2 x 3,14 x 15 cm = 94,2 cm.
Tentukan keliling lingkaran yang panjang jari-jarinya 36 cm dan π = 3,14.
Keliling = 2πr = 2 x 3,14 x 36 cm = 226,08 cm.
Tentukan keliling lingkaran yang panjang jari-jarinya 15,5 cm dan π = 3,14.
Keliling = 2πr = 2 x 3,14 x 15,5 cm = 97,34 cm.
Diameter mata uang koin lima ratus rupiah adalah 15 mm. Hitunglah kelilingnya.
Keliling = 2πr = 2 x 3,14 x 15 mm = 94,2 mm.
Diameter sebuah roda mobil adalah 42 cm. Hitunglah keliling roda tersebut.
Keliling = πd = 22/7 x 42 cm = 22 x 6 cm = 132 cm.
Rumus Keliling Lingkaran
Merujuk pada Buku Kumpulan 100 Soal Hots dan Pembahasan Bangun Datar dari Penerbit CV Madani Jaya, lingkaran mempunyai sifat-sifat meliputi terdapat sebuah titik pusat, terdiri dari satu sisi, tidak memiliki titik sudut dan jumlah sudutnya 360 derajat, mempunyai jari-jari (r) dan diameter (d), serta simetri lipat dan simetri putar tidak terhingga.
Baca berita dengan sedikit iklan, klik di sini
Adapun rumus keliling lingkaran sebagai berikut:
Hubungan Roda-Roda Sepusat
Kalau di awal gue udah bahas sedikit tentang rantai dan gir sepeda, sekarang gue mau ajak elo buat lihat contoh lainnya. Gir dan ban sepeda motor bagian belakang adalah salah satu contoh yang bisa menjelaskan apa itu hubungan roda sepusat.
Saat naik sepeda motor, mungkin elo pernah berpikir gimana caranya motor itu bisa berjalan. Selain karena bantuan mesin dan bahan bakar minyak, ban motor juga bergerak karena menerapkan konsep hubungan roda-roda.
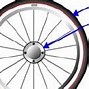
Coba deh, elo amati baik-baik gambar di bawah ini.
Dari gambar, terlihat jelas kalau ban dan gir merupakan hubungan roda-roda sepusat. Di sini, gir bisa disebut juga sebagai roda karena berbentuk piringan pipih. Keduanya dihubungkan dengan satu poros yang berada di tengah ban dan gir.
Biar lebih jelas, gue kasih ilustrasi yang lebih sederhana, ya. Di bawah ini, roda berwarna ungu merupakan ban sepeda motor, roda berwarna kuning merupakan gir, dan lingkaran hitam kecil adalah pusat roda-roda.
Meskipun kedua roda tersebut ada di satu pusat yang sama, keduanya punya ukuran yang berbeda. Begitu juga dengan jari-jari mereka. Jari-jari roda kuning (RA) akan lebih kecil dari jari-jari roda ungu (RB).
Sekarang pertanyaannya, kalau gue putar roda ungu ke kanan, apa yang akan terjadi dengan roda kuning? Tentu aja, roda kuning akan ikut berputar ke arah yang sama dengan roda ungu karena keduanya mempunyai satu pusat yang sama.
Dari ilustrasi tersebut, udah paham kan hubungan roda-roda sepusat tuh kayak gimana?
Baca Juga: Pengertian Gaya Sentripetal dan Sentrifugal Beserta Rumusnya – Materi Fisika Kelas 10
Hubungan Roda-Roda dengan Rantai
Hubungan roda-roda selanjutnya masih berkaitan sama contoh yang udah gue sebutkan di atas. Yup, salah satu penerapan hubungan roda-roda dengan rantai ada pada gir belakang dan gir depan sepeda.
Coba kita balik lagi ke penjelasan rantai, gir, dan roda sepeda tadi, ya. Posisi gir depan menempel dengan pedal sepeda dan terhubung oleh rantai. Saat elo gowes pedal sepeda, gir depan akan berputar dan menggerakkan gir belakang yang juga tersambung ke rantai.
Hampir mirip motor, gir belakang juga menempel dengan ban belakang sepeda secara sepusat. Karena itulah, bagian belakang gir pada sepeda menggunakan prinsip roda dan poros yang terhubung oleh rantai.
Secara sederhana, gambaran hubungan roda-roda dengan rantai pada gir sepeda bisa elo perhatikan lewat gambar berikut.
Pada ilustrasi di atas, roda kuning mewakili gir belakang sepeda yang punya ukuran jari-jari lebih kecil (RA). Sementara, roda ungu adalah gir depan sepeda yang ukuran jari-jarinya lebih besar (RB).
Nah, dari penjelasan dan ilustrasi ini, apakah elo udah bisa menebak bagaimana bentuk persamaan untuk hubungan roda-roda dengan rantai?
Baca Juga: Ruang Lingkup Fisika Kelas 10, Belajar Apa sih di Fisika?
Setelah belajar tentang gerak melingkar, GLB, dan percepatan sentripetal, di subbab materi Fisika kelas 10 selanjutnya, elo perlu memahami bagaimana hubungan roda-roda yang menyebabkan suatu roda berputar.
Aduh! Lagi asyik keliling komplek naik sepeda, rantai rodanya malah copot!
Siapa yang pernah ngalamin hal kayak di atas? Tenang, elo nggak sendirian. Rantai sepeda gue pun beberapa kali lepas. Akhirnya, gue terpaksa turun dan mendorong sepeda gue ke bengkel.
Tapi, karena kejadian itu, gue jadi memperhatikan gimana pedal yang gue genjot bisa menggerakkan rantai dan gir, sampai kemudian membuat roda berputar. Dalam Fisika, konsep ini dikenal dengan istilah hubungan roda-roda.
Di subbab sebelumnya, elo udah belajar tentang gerak melingkar. Masih ingat, kan? Nah, hubungan roda-roda inilah yang menjadi salah satu bentuk penerapannya.
Materi ini membahas bagaimana suatu roda dengan roda yang lainnya bisa terhubung dan menggerakkan satu sama lain. Mau tahu penjelasannya lebih dalam? Yuk, kita bahas bareng-bareng!
Rumus Hubungan Roda-Roda Bersinggungan
Seperti yang gue tuliskan, pada hubungan roda-roda ini, ada satu titik bersinggungan yang menyebabkan kedua roda berputar secara bersamaan. Di titik inilah, besar kecepatan linear kedua roda akan sama.
Jadi, meskipun kedua roda punya arah kecepatan sudut yang berlawanan, besar kecepatan linearnya tetap sama. Karena itu, persamaan hubungan roda-roda ini akan sama dengan roda berantai, yaitu:
VA = kecepatan linear gir kecil atau roda kuning
VB= kecepatan linear gir besar atau roda ungu
⍵A = kecepatan sudut roda kecil atau roda kuning
⍵B = kecepatan sudut roda besar atau roda ungu
RA= jari-jari gir kecil atau roda kuning
RB= jari-jari gir besar atau roda ungu
Oh iya, karena hubungan roda-roda bersinggungan mempunyai gerigi, jumlahnya akan mempengaruhi kecepatan perputaran roda. Semakin banyak gerigi pada roda-roda, maka perputarannya akan semakin melambat.
Bagi Sobat Zenius yang mau memperdalam materi ini, elo bisa tonton video-video penjelasannya di Zenius. Caranya, elo tinggal klik banner yang ada di bawah ini.
Contoh Soal Hubungan Roda-Roda
Setelah tahu pengertian dan rumus hubungan roda-roda, nggak lengkap rasanya kalau elo belum latihan soal. Jadi, langsung aja cek contoh-contoh soalnya di bawah ini, yuk!
Dua buah silinder seporos diputar dengan kecepatan sudut konstan. Perbandingan jari-jarinya 5:3. Jika kecepatan linear silinder besar adalah 5 m/s, maka kecepatan linear silinder kecil adalah …. m/s.
Karena dalam soal disebutkan silinder seporos, artinya elo perlu menggunakan persamaan hubungan dua roda sepusat, yaitu ⍵A = ⍵B.
Di sini, perbandingan jari-jari kedua silinder udah diketahui sebesar 5:3, dengan kecepatan linear silinder besar adalah 5 m/s. Jadi, elo bisa langsung substitusi nilai-nilai tersebut ke dalam persamaannya seperti berikut.
Oke, udah jelas, ya, jawaban yang sesuai adalah c. 3.
Perhatikan gambar hubungan roda-roda berikut ini!
Roda C diputar dengan kecepatan linear tetap sebesar 5 m/s perbandingan jari-jari roda A, B, C dan D adalah 3:5:6:9. Kecepatan linear roda B adalah … m/s.
Kalau dihadapkan dengan hubungan roda-roda yang cukup kompleks kayak gini, elo bisa fokus ke roda-roda yang nilainya udah diketahui, yaitu roda C yang mempunyai kecepatan linear sebesar 5 m/s dan perbandingan jari-jarinya 6.
Dari gambar, roda yang terhubung secara langsung dengan roda C adalah roda D. Jadi, elo perlu cari tahu dulu hubungan keduanya. Menurut elo, apa hubungan antara roda C dan D?
Iya, roda C dan D terhubung secara sepusat. Berarti kecepatan sudut di antara keduanya adalah sama.
Oke, sekarang elo udah dapat kecepatan linear roda D sebesar 45/6 m/s. Selain dengan roda C, roda D juga terhubung secara langsung sama roda A. Pada kasus ini, roda D dan roda A terhubung dengan tali atau rantai. Jadi, bentuk persamaannya adalah VD= VA.
Nah, di perhitungan sebelumnya, elo udah berhasil menemukan nilai VD, yaitu 45/6 m/s. Artinya, kecepatan linear dari roda A juga sebesar nilai tersebut.
Selanjutnya, elo perlu cari roda lain yang berhubungan langsung dengan roda A. Di sini, roda A terhubung secara sepusat dengan roda B. Karena itu, elo bisa menghitungnya dengan persamaan berikut.
Sehingga, pilihan yang tepat untuk menjawab soal ini adalah b. 12,5.
Di bawah ini yang merupakan contoh roda bersinggungan adalah ….
a. Gir depan dan gir belakang sepeda.
b. Roda bergerigi pada correction tape.
c. Ban belakang sepeda motor.
d. Roda pada bus dan mobil.
Roda bersinggungan adalah dua atau lebih roda saling menempel atau bersinggungan satu sama lain. Contoh hubungan roda-roda ini bisa elo temukan pada mesin kendaraan bermotor, mesin jam tangan, dan correction tape.
Elo pasti tahu, kan, apa itu correction tape? Iya, alat ini punya fungsi yang sama seperti tipe x, tapi secara penggunaan lebih efisien.
Di dalam correction tape, ada dua roda dengan susunan bersinggungan yang tersambung dengan pita koreksi. Pas elo pakai, pita koreksi akan bergesekan dengan kertas dan memutar roda yang jari-jarinya lebih besar.
Karena ada gerigi yang bersinggungan, roda kecil kemudian ikut memutar dengan arah yang berlawanan dengan roda besar. Sampai akhirnya, perputaran roda kecil menyebabkan pita koreksi bekas kembali tergulung secara rapi.
Dari penjelasannya bisa kita simpulkan kalau jawaban yang tepat adalah b. Roda bergerigi pada correction tape.
Gimana? Jadi lebih gampang dipahami, kan, kalau udah latihan contoh-contoh soalnya?
Oke, segitu dulu pembahasan kita tentang hubungan roda-roda. Mulai dari pengertian, jenis-jenis, rumus, sampai contohnya di kehidupan sehari-hari.
Kalau elo mau mempelajari materi Fisika kelas 10 lainnya, elo bisa cek video-video belajar yang ada di Zenius. Langsung aja, klik link yang ada di bawah ini, ya!
Materi Fisika Kelas 10
Hubungan Antarroda – Materi Zenius Kelas 10
Fisika Dasar 1 – Heri Kiswanto (2022)
Fisika Sekolah I Berkarakter Berbasis Model POE2WE untuk Menghadapi Abad 21 – Dr. Nana, M.Pd. (2019)
Bedah Fisika Dasar – Kurrotul Ainiyah (2018)
Download nowDownloaded 367 times
TEMPO.CO, Jakarta - Lingkaran adalah salah satu bentuk bangun datar yang berjarak sama terhadap satu titik tertentu. Titik tertentu yang dimaksud berada tepat di tengah lingkaran yang disebut sebagai titik pusat lingkaran.
Penentuan luas dan keliling lingkaran umumnya muncul dalam mata pelajaran Matematika sejak duduk di bangku kelas empat sekolah dasar (SD). Lantas, bagaimana rumus keliling lingkaran?
Hubungan Roda-Roda Bersinggungan
Hubungan roda-roda yang terakhir adalah bersinggungan. Kira-kira, elo kebayang, nggak, gimana bentuknya?
Sebenarnya, hubungan roda-roda bersinggungan banyak banget elo temukan di kehidupan sehari-hari. Contohnya pada mesin jam analog atau pada gir mesin motor.
Namanya juga bersinggungan, artinya kedua atau lebih roda itu saling menempel satu sama lain. Selain ukurannya yang berbeda, setiap roda juga punya gerigi yang bertujuan sebagai pengikat pinggiran roda. Sehingga, antarroda bisa bergerak bersama-sama.
Lebih jelasnya, elo bisa lihat gambar hubungan roda-roda bersinggungan di bawah ini.
Dalam gambar, roda ungu mewakili gir yang lebih besar, sedangkan roda kuning merupakan gir yang lebih kecil. Saat roda ungu berputar ke kanan, ada satu titik bersinggungan yang menyebabkan roda kuning ikut berputar.
Tapi, arah perputaran roda kuning akan berbeda dengan roda ungu. Elo udah ada bayangannya, kan? Kalau roda ungu berputar ke kanan, roda kuning akan berputar ke kiri. Begitu juga sebaliknya. Dengan kata lain, kedua roda akan berputar ke arah yang berlawanan.
Baca Juga: Rumus Dimensi dalam Fisika Beserta 9 Contoh Soal
Rumus Hubungan Roda-Roda dengan Rantai
Dalam hubungan roda-roda dengan rantai, ketika sepeda bergerak maju, gir depan dan gir belakang sepeda akan berputar searah jarum jam. Artinya, arah kecepatan sudut kedua gir adalah sama.
Tapi, karena gir depan dan gir belakang sepeda terhubung dengan rantai, gerakan keduanya juga menimbulkan kecepatan linear. Hal ini disebabkan karena adanya singgungan antara gir dan rantai.
Sedikit berbeda dengan hubungan roda-roda sepusat, roda yang dihubungkan dengan rantai akan mempunyai arah dan besar kecepatan linear yang sama. Dengan kata lain, bentuk persamaan awalnya bisa ditulis seperti berikut.
VA = kecepatan linear gir belakang atau gir kuning
VB = kecepatan linear gir depan atau gir ungu
Sementara itu, diketahui rumus untuk menghitung kecepatan linear adalah kecepatan sudut dikali dengan jari-jari roda. Jadi, rumus ini bisa langsung elo substitusikan ke persamaan sebelumnya, yaitu:
VA = kecepatan linear gir kecil atau roda kuning
VB= kecepatan linear gir besar atau roda ungu
⍵A = kecepatan sudut roda kecil atau roda kuning
⍵B = kecepatan sudut roda besar atau roda ungu
RA= jari-jari gir kecil atau roda kuning
RB= jari-jari gir besar atau roda ungu
Baca Juga: Pengertian, Fungsi, dan Cara Menggunakan Jangka Sorong – Materi Fisika Kelas 10